Algorithm
The algorithm can detect corners and edges effectively. It uses structural information from the structure tensor’s eigenvalues to find change in intensity values and their direction. A much detailed explanation can be found at Harris Corner Detection.
Implementation
I will be implementing the algorithm in Python using NumPy and I will use the following image to demonstrate.

Source Code
The full project code is available at GitHub.
Image Derivatives
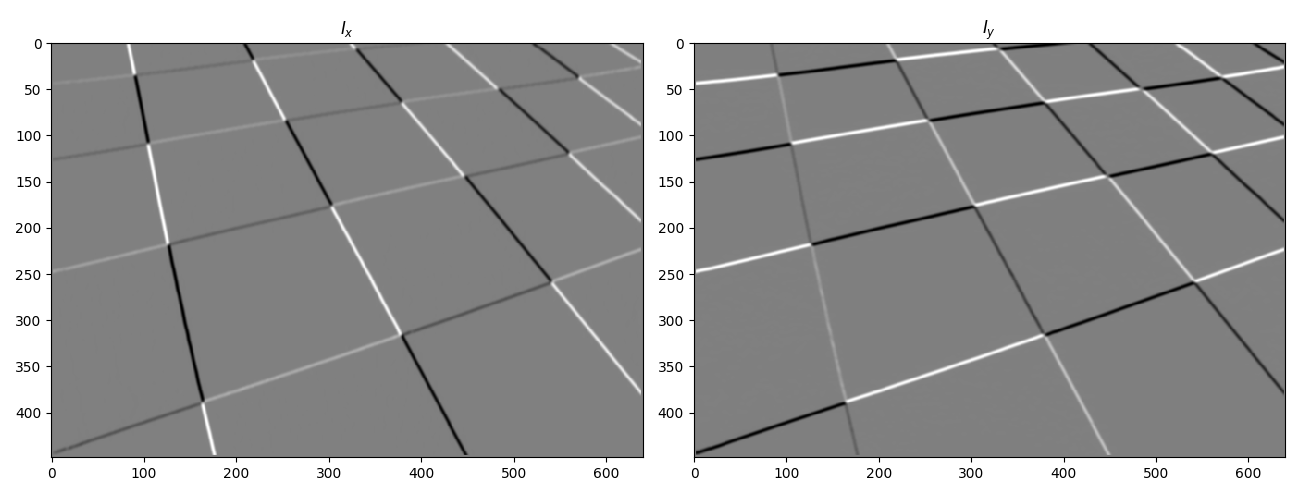
We’ve used Sobel operators of aperture 3 to compute \(I_x\) and \(I_y\) . Since the Sobel operators are seperable filters (have rank 1), we have used the optimised algorithm for calculating the derivatives. We define the following function to filter an image $I$ with a seperable filter whose factors are filter_y\(_{(1×3)}\) and filter_x\(_{(3×1)}\)
def seperable_conv(I, filter_x, filter_y):
h, w = I.shape[:2]
n = filter_x.shape[0]//2
I_a = np.zeros(I.shape)
I_b = np.zeros(I.shape)
for x in range(n, w-n):
patch = I[:, x-n:x+n+1]
I_a[:, x] = np.sum(patch * filter_x, 1)
filter_y = np.expand_dims(filter_y, 1)
for y in range(n, h-n):
patch = I_a[y-n:y+n+1, :]
I_b[y, :] = np.sum(patch * filter_y, 0)
return I_b
Now, for Sobel derivatives, we just take the filters as \([−1, 0, 1] , [1, 2, 1]^T\) and vice-versa.
def detect(I, n_g, n_w, k):
h, w = I.shape
sobel_1 = np.array([-1, 0, 1])
sobel_2 = np.array([1, 2, 1])
I_x = seperable_conv(I, sobel_1, sobel_2)
I_y = seperable_conv(I, sobel_2, sobel_1)
...
We now apply gaussian blur to smoothen the image. Since gaussian filter is also seperable, we take advantage of this fact and use the above function.
def gaussian_mask(n, sigma=None):
if sigma is None:
sigma = 0.3 * (n // 2) + 0.8
X = np.arange(-(n//2), n//2+1)
kernel = np.exp(-(X**2)/(2*sigma**2))
return kernel
def detect(I, n_g, n_w, k):
...
g_kernel = gaussian_mask(n_g)
I_x = seperable_conv(I_x, g_kernel, g_kernel)
I_y = seperable_conv(I_y, g_kernel, g_kernel)
D_temp = np.zeros((h,w,2,2))
...
Structure Tensor
\begin{align} \left.A = \sum_{u}\sum_{v}w(u,v)\begin{bmatrix} I_x^2 & I_xI_y \\I_xI_y & I_y^2\end{bmatrix} \right |_{u,v} \end{align}
Using the smoothened derivatives \(I_x, I_y\), we calculate the structure tensor \(A\) at every pixel.
def detect(I, n_g, n_w, k):
...
D_temp = np.zeros((h,w,2,2))
D_temp[:,:,0,0] = np.square(I_x)
D_temp[:,:,0,1] = I_x*I_y
D_temp[:,:,1,0] = D_temp[:,:,0,1]
D_temp[:,:,1,1] = np.square(I_y)
g_filter = gaussian_mask(n_w)
g_filter = np.dstack([g_filter]*4).reshape(n_w, 2, 2)
D = seperable_conv(D_temp, g_filter, g_filter)
...
Eigenvalues
Since A is a \(2×2\) matrix. It’s eigenvalues have a closed form solution.
Let,
\begin{align} A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \end{align}
Then,
\begin{align} \lambda_{1,2} = \frac{a+d}{2}\pm\frac{\sqrt{(a-d)^2+4bc}}{2} \end{align}
def detect(I, n_g, n_w, k):
...
P = D[:, :, 0, 0]
Q = D[:, :, 0, 1]
R = D[:, :, 1, 1]
T1 = (P+R)/2
T2 = np.sqrt(np.square(P-R)+4*np.square(Q))/2
L_1 = T1-T2
L_2 = T1+T2
...

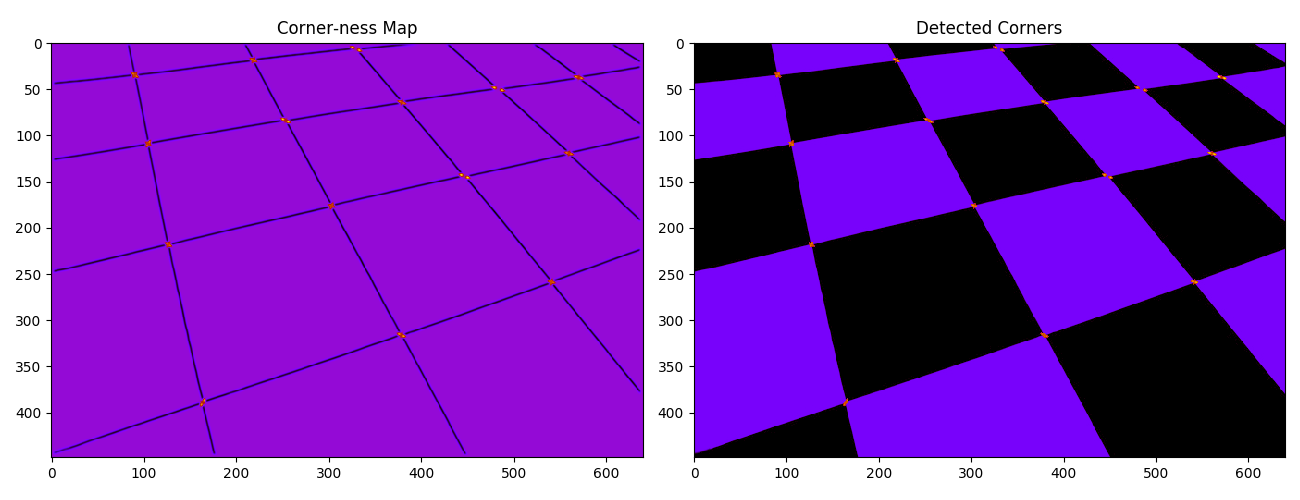
Cornerness Measure
Cornerness measure \(C\) was calculated and thresholded at \(0.457\) (found emperically).
\begin{align}
C = \lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2
\end{align}
Comments